악상 해석과 표현의 기초: 책 머리에

102 page ~ 104 page.

아티큘레이션의 유형1, 운율적 아티큘레이션

　운율적 패턴과 구문적 구조 그리고 표현적 요소, 이 세 가지는 아티큘레이션을 형성하는 세 축이라 하겠습니다. 리만(Hugo Riemann)의 이론은 그중에서 「운율적 패턴에 의한 아티큘레이션」의 원리에 잘 부합됩니다 . 이미 이야기한 바 있듯 리만의 이론은 여린내기의 운율, 즉 약강격인 아이앰(iamb)과 약약강격인 아나페스트(anapest) 그리고 약강약격인 앰피브랰(amphibrach)의 음보(foot)를 적용하여 선율의 구조를 파악하는 것이 그 핵심입니다. 이하, 리만의 이론을 원용(援用)하여 운율적 아티큘레이션(metrical articulation, foot-style articulation)의 이치를 설명하도록 합니다. 특히, 서양음악의 주류라 할 고전 및 낭만파 음악은 이와 같은 운문(韻文)적인 리듬을 주체로 하고 있습니다. (그러나, 그와 반대로 16세기 음악의 리듬은 산문적이어서 박자 감이 약하며, 산문적인 리듬을 중시하는 경향은 19세기 후반 바그너의 후기 작품에서도 엿볼 수 있습니다).

⊙ 음가(音價)가 짧은 음(들)은 뒤에 오는 음가가 긴 음에 연결하여 그루핑합니다(보기7). 그리하여 음가가 짧은 음들이 음가가 긴 음을 향해 힘을 실어 가도록 합니다. 이는 서양 언어와 음악의 자연스런 운율이자 억양입니다.

보기7. 그루핑 원리 ― 음가가 짧은 음(들)은 뒤에 오는 긴 음에 연결

여린내기 운율적 아티큘레이션의 그루핑 패턴

⊙ 음악의 1박을 음보의 1음절로 간주하고, 여린박을 뒤에 오는 센박에 연결하는 식으로 하여 2, 3, 4박 계열의 음보를 만들면, 그것이 그대로 여린내기 운율적 아티큘레이션의 전형적인 그루핑 패턴이 됩니다(보기8).

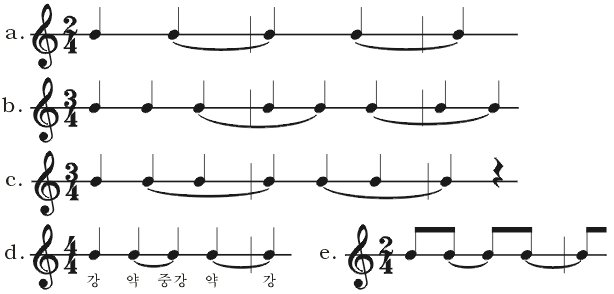
보기8. 여린내기 운율적 아티큘레이션의 전형적인 그루핑 패턴

　보기8의 a, d, e는 약강격(iamb), b는 약강약격(amphibrach), c는 약약강격(anapest)의 운율 패턴(음보)에 해당합니다.

　3박 계열은 강·약·약으로 여린박이 2개이므로 곡의 문맥에 따라 두 가지의 패턴이 가능합니다(보기8.b 또는 c). 그러나 보기8.c보다는 보기8.b 쪽이 보다 통상적입니다. 4박 계열은 강·약·중강·약의 리듬을 가지므로 제3박은 센박으로 간주하여 그루핑합니다(보기8.d).

　2박 계열일지라도 음이 세분되어 가령 반박(박) 위주의 음렬로 되어 있고 속도가 느릴 때는 반박을 마치 한 박(음보의 한 음절)인 것처럼 간주하여 4박 계열의 패턴을 적용·그루핑하기도 합니다(☞ ※ p.104, 참고: 박의 분할과 겹박자). 이를테면, 2/4박에서의 8분음표(반박)의 음렬을 마치 4/8박에서의 8분음표(한 박)의 음렬인 것처럼 취급하여 4박 계열의 패턴으로 그루핑하는 것입니다(보기8.e, 악보78, 악보79).

악보78. 마적 주제에 의한 변주곡(Var. sur L'air) ― F. Sor, Op.9, 기타곡(전곡 ☞ p.322)

※ 이음줄 아래 스타카토 점이 표시된 메조·스타카토 기호는 붙임줄(tie)로 해석되는 오해를 피하기 위한 것입니다(※ ☞ p.22, 참고: 동음 간의 이음줄).

악보79. 환상곡(Fantaisie) ― F. Sor, Op. 7, 기타곡(전곡 ☞ p.321)

　이처럼 「박의 분할」이나 곡의 빠르기에 따라 그루핑의 단위가 되는 음가(또는 박의 길이)가 달라질 수 있습니다 ― 연주 속도가 빠르면 보다 긴 음가의 음이, 연주 속도가 느리면 보다 짧은 음가의 음이 그루핑의 단위가 될 수 있습니다.

　아래 보기9.a는 통상적인 4/4박의 그루핑 형태입니다만, 만일 속도가 빨라지면 곡의 내용에 따라서는 보기9.b와 같은 그루핑이 적절할 수도 있습니다. 보기9.b의 그루핑은 사실상 2/2박의 그루핑 패턴에 해당합니다. 즉, 2박 계열의 그루핑인 것입니다. 4/4박은 2/2박에 있어서의 각 박이 '반박(半拍) 단위로 분할된 형태'와 같습니다(☞ ※ 아래, 참고: 박의 분할과 겹박자 중 보기14).

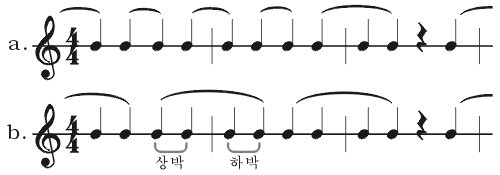
보기9. 속도에 따른 그루핑 패턴의 변화

　보기9.b를 보기10과 같이 2/4박으로 바꾸어 보면 보다 이해가 쉽습니다.

보기10. 2박 계열의 그루핑